El matemático y el vendedor ambulante
Esta entrada participa en la Edición 12.4: “Quod Erat Demonstrandum” del Carnaval de Matemáticas, organizado en esta ocasión por la Asociación de Estudiantes QED.
Table of contents:
Acto I. El problema del viajante.
Vendedor ambulante.- ¡Por fin te encuentro, matemático! ¡Tengo un gran problema!
Matemático.- ¿Qué ocurre?
Vendedor ambulante.- Me gustaría vender mis hortalizas a lo largo de toda la península, pero pierdo mucho tiempo haciéndolo. Necesito que me encuentres un camino eficiente para poder vender todos mis productos lo más rápido posible. Además, ya sé lo que tardo en moverme de una ciudad a otra, así que lo tienes fácil.
Matemático.- ¡¿Toda la península?!
(Más tarde)
Matemático.- Creo que se me puede ocurrir algo…
El matemático necesita encontrar un camino que atraviese todas y cada una de las ciudades que le ha indicado su amigo el vendedor ambulante:
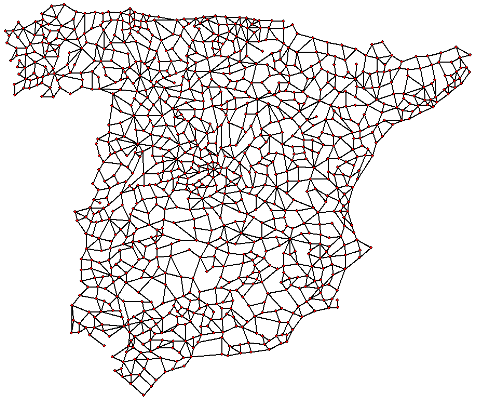
Por supuesto, el vendedor vive en una de las ciudades, de la que saldrá al iniciar su ruta, y a la que volverá tras acabarla. Lo primero que observó el matemático, es que en la ruta no habrá ciudades repetidas, puesto que si el vendedor ambulante ya ha hecho negocios en una de ellas, difícilmente reunirá más clientes si pasa una segunda vez.
El matemático se pone manos a la obra, y decide utilizar un grafo para representar el problema. Primero, representa cada ciudad con un círculo que llama vértice, y después, conecta cada uno de los pares de ciudades con una línea llamada arista. En cada arista, asimismo, el matemático escribe cuánto tarda el vendedor en ir entre las dos ciudades. Este es un ejemplo para un menor número de ciudades:

Como el matemático ha conectado cada par de ciudades, para poder así tener en cuenta todas las posibilidades de movimientos, el grafo resultante es, según él dice, “completo”, es decir, existe una conexión entre cada par de vértices.
El objetivo del matemático ahora es encontrar un ciclo en el grafo, es decir, una sucesión de vértices a partir de uno dado, que además incluya todos los vértices una única vez y vuelva al punto de partida tras ello. Esto se traducirá en la ruta deseada para el vendedor ambulante. Un ciclo así, dice el matemático, se llama ciclo “Hamiltoniano”.
Encontrar una ruta con esas características es muy fácil: como cada vértice se conecta con todos los demás, se puede empezar en un vértice y elegir cualquiera de los restantes como siguiente destino, repitiendo hasta quedarse sin ciudades por visitar. Finalmente, se volvería al vértice de origen. Por ejemplo, en el grafo anterior, un posible ciclo sería Euleria - Reino de Möbius - Ciudad Gauss - Numerasia - Euleria. No obstante, si sumamos lo que tarda el vendedor ambulante en recorrerlo, llegamos a \(11+5+7+5 = 28\).
El matemático rápidamente se da cuenta de que, visitando Ciudad Gauss y Numerasia antes que el Reino de Möbius, en lugar de después, el vendedor ambulante tardaría \(5+7+1+11 = 24\), es decir, menos. El objetivo está claro. El matemático llama coste a la suma de los tiempos de cada arista, y enuncia:
Problema del viajante. Dado un grafo completo, encontrar un ciclo Hamiltoniano de coste mínimo.
Quizás en el grafo de ejemplo sea fácil de obtener, pero el matemático ve imposible atacar el problema para todas las ciudades de la península. ¡Hay muchísimas combinaciones! Al matemático, sin embargo, se le ocurre una manera inteligente de encontrar un trayecto bastante bueno.
Matemático.- El trayecto debería utilizar las aristas más baratas. No es posible que, si entre dos ciudades se tarda en viajar un minuto, no sean visitadas en sucesión.
Para ilustrar el ejemplo, el matemático utiliza este grafo un poco más complicado que el anterior:
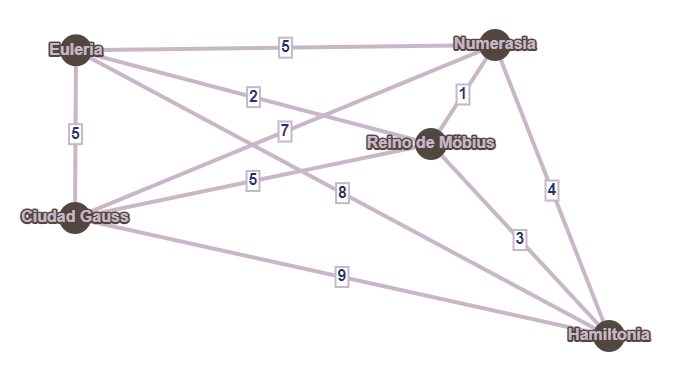
Ahora, el matemático marca las aristas más baratas, para darles prioridad. Esto lo hace en orden, es decir, primero marca la arista que cuesta \(1\), luego la que cuesta \(2\) y así sucesivamente. Al hacerlo, tiene cuidado de no repetir ciudades: si alguna arista le obligase a visitar ciudades repetidas (es decir, si crea un ciclo que no pasa por todas las ciudades), se la salta. Este es el resultado:
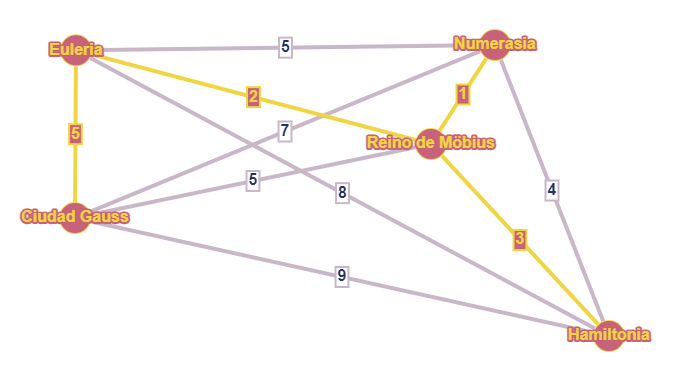
Como habíamos anticipado, el matemático se ha tenido que saltar la arista de distancia \(4\) entre Numerasia y Hamiltonia, puesto que habría cerrado el ciclo antes de tiempo. De hecho, ya no puede añadir ninguna arista más sin que eso ocurra.
(Clic para saber más)
El matemático ha ejecutado lo que se conoce como el algoritmo de Kruskal, que permite obtener un grafo sin ciclos dentro de otro grafo dado, con suma de distancias mínima. Este nuevo grafo se conoce como árbol recubridor mínimo.
El matemático está convencido de que estaría bien utilizar esas aristas, aunque sabe que no va a poder usar todas, porque necesita que el camino empiece y termine en el mismo vértice. Una buena manera de hacerlo, se le ocurre, es la siguiente. Partimos de las aristas marcadas:
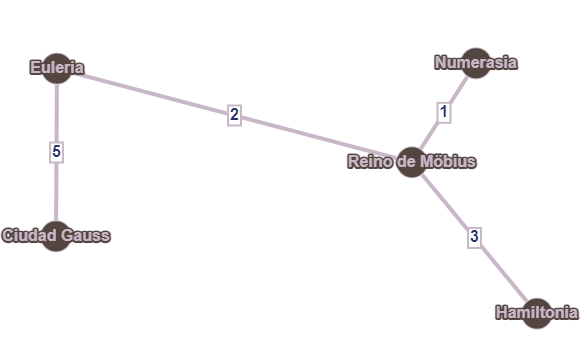
El matemático no sabe muy bien cómo encontrar un ciclo Hamiltoniano añadiendo pocas aristas, pero recuerda de su época de estudiante un teorema que le permite encontrar un ciclo en el grafo que pase por todas las aristas una única vez (aunque podría pasar varias veces por un vértice). Para ello, necesita que el número de aristas conectadas con cada vértice sea par, así que añade algunas más para que así sea:
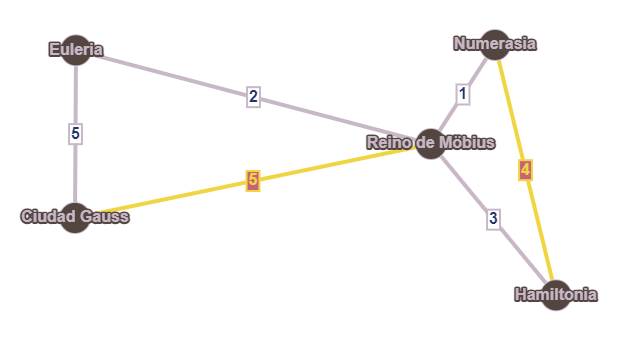
Ahora ya puede encontrar un ciclo como el descrito anteriormente, y así lo hace: Euleria - Reino de Möbius - Numerasia - Hamiltonia - Reino de Möbius - Ciudad Gauss - Euleria. Como había anticipado, una de las ciudades se repite, pero simplemente se la salta la segunda vez, para evitarlo. Esto da lugar al siguiente trayecto final:
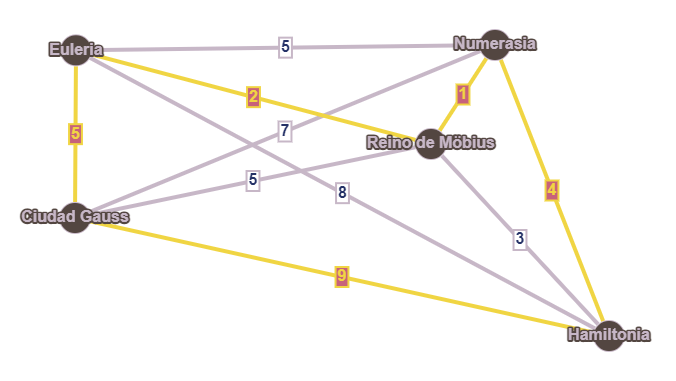
El coste es de \(2+1+4+9+5 = 21\). El matemático está bastante contento con este resultado, y se dispone a aplicarlo en el mapa del vendedor ambulante. ¡Qué alivio!
(Clic para saber más)
El matemático ha seguido paso a paso el algoritmo de Christofides para resolver el problema del viajante. Este algoritmo no garantiza que el resultado sea óptimo, dado que esto es extremadamente difícil en general. Sin embargo, garantiza que el coste final no superará en más de un 50% el coste óptimo.
Acto II. El orden de los factores.
Matemático.- ¡Cuánto tiempo, vendedor! ¿Qué tal va la ruta que calculé para ti? ¿Está siendo beneficiosa?
Vendedor ambulante.- Verás…
Matemático.- (Espero que no sea otro encargo imposible)
Vendedor ambulante.- Ha ocurrido un imprevisto. Cuando yo calculé el tiempo que me costaba ir entre Madrid y Segovia, puse el cronómetro en Madrid y lo paré en Segovia.
Matemático.- Es razonable.
Vendedor ambulante.- Sin embargo, en tu ruta no voy de Madrid a Segovia, sino de Segovia a Madrid. Por algún motivo que no entiendo, ¡tardo más si voy al revés!
Matemático.- ¿Será por el desnivel? ¿O quizás el tráfico? ¿Tienes que pasar peajes solo en una de las direcciones?
Vendedor ambulante.- No tengo ni idea, pero estás de enhorabuena. He calculado los tiempos en ambos sentidos para todas las ciudades. Ahora, es tu momento de encontrarme otra ruta mejor.
Matemático.- (Creo que esto es lo contrario de estar de enhorabuena…)
El matemático se ha encontrado con un nuevo problema, aún más difícil si cabe. Ahora, el coste entre vértices depende del sentido de recorrido. Por tanto, ya no podrá usar su técnica de utilizar un grafo, al menos no como el que usaba antes. Por fortuna, al matemático se le ha ocurrido una posible idea.
Primero, va a poner dos aristas entre cada par de vértices, una en cada sentido. Para representar esto, utiliza flechas en vez de líneas. Esto le permite registrar los nuevos costes, en un grafo que él llama “dirigido”:
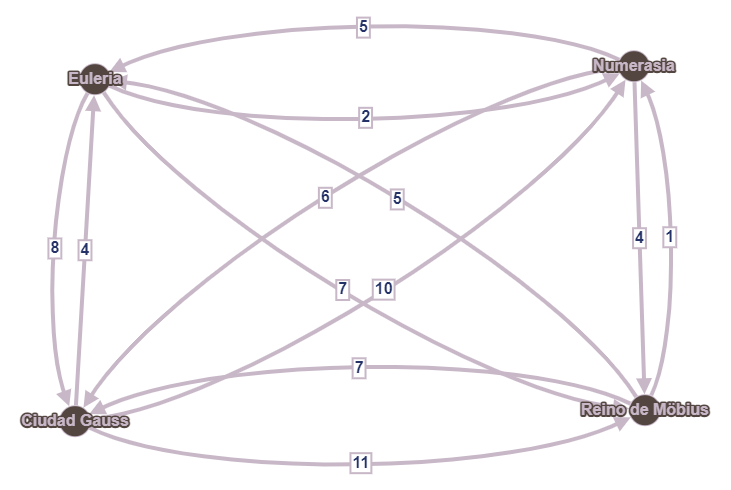
¡Qué complicado! Ahora tiene muchas más aristas con las que trabajar, no sabe si el procedimiento que siguió antes va a funcionar y cada arista solo puede recorrerse en el sentido de la flecha, y no al revés.
Problema del viajante asimétrico. Dado un grafo completo dirigido, encontrar un ciclo Hamiltoniano de coste mínimo.
Matemático.- No tiene ningún sentido que vuelva a partir de cero. Ya he resuelto un problema parecido en el pasado, cuando el grafo no era dirigido. Si consigo convertir este grafo en uno que no sea dirigido, pero que represente el mismo problema, habré terminado. Pero, ¿cómo?
De repente, el matemático tiene una idea brillante. Va a ver el problema desde otra perspectiva. Desde una perspectiva en la que se obtiene un grafo no dirigido.
Matemático.- Ya lo tengo. Voy a hacer que cada vértice no represente una ciudad, sino el hecho de entrar en una ciudad. También voy a añadir otro vértice que represente el hecho de salir de una ciudad.
Lo que quiere decir el matemático, es que va a convertir la ciudad de Euleria en dos vértices: EntrarEuleria y SalirEuleria. Aunque esto pueda parecer que no tiene sentido, la idea está clara con un ejemplo. Supongamos que tenemos este grafo tan sencillo:
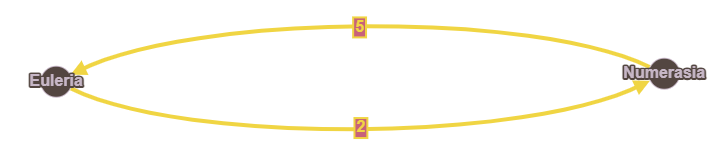
El ciclo óptimo es, evidentemente, Euleria - Numerasia - Euleria. Si ponemos en práctica la idea del matemático, podemos convertirlo en este grafo que representa el mismo problema, pero ahora no es dirigido:
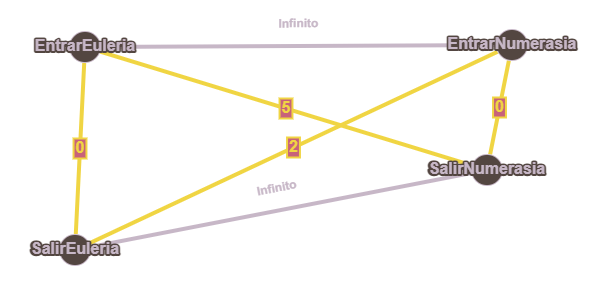
Por supuesto, si salimos de Euleria para entrar a Numerasia, el coste es \(2\), y si salimos de Numerasia para entrar en Euleria, el coste es \(5\). El coste entre entrar y salir de una misma ciudad es \(0\), porque no estamos recorriendo camino en el proceso. Por otro lado, el coste de conexiones imposibles, como salir de Euleria y después salir de Numerasia (sin haber entrado), será de infinito, y así no aparecerá en la solución mínima.
Vemos también que el ciclo Hamiltoniano óptimo es ahora EntrarEuleria - SalirEuleria - EntrarNumerasia - SalirNumerasia. Esto se traduce fácilmente a Euleria - Numerasia, en cuanto al orden de ciudades se refiere. El coste sigue siendo \(5+0+2+0 = 7\).
Este procedimiento aplicado a cada par de nodos permite transformar el problema del viajante asimétrico en el problema del Acto I.
Matemático.- Ahora ya puedo aplicar lo que hice el otro día, cuando el grafo no era dirigido, y darle al vendedor la ruta que necesita. No hay problema que un matemático no pueda resolver…
Acto III. La suma de las partes.
Vendedor ambulante.- Ese es… ¡Sí! ¡Oye, matemático! ¡Soy yo!
Matemático.- No es posible, me ha visto…
Vendedor ambulante.- Quería darte las gracias por la ruta que calculaste. ¡Estoy ganando dinero de manera desorbitada!
Matemático.- ¡Me alegro! ¿Cuánto me toca?
Vendedor ambulante.- No venía a verte por eso. Quería decirte que he contratado a dos empleados más. ¡Así puedo vender la mercancía mucho más rápido!
Matemático.- Oh, no…
Vendedor ambulante.- ¿Qué te parece si me encuentras tres rutas, una para cada uno de nosotros, que nos permitan visitar entre los tres todas las ciudades de manera eficiente?
Matemático.- Veré lo que puedo hacer.
Una vez más, es hora de codificar este problema mediante un grafo. Ahora que hay tres empleados, una solución ingenua sería coger el trayecto que ya conocíamos, para una persona, y dividirlo entre tres. Pero esto no es posible: los empleados del vendedor ambulante viven en la misma ciudad que él. Es decir, los tres deben comenzar y acabar en la misma ciudad. Por supuesto, tampoco tiene sentido que dos empleados pasen por la misma ciudad. Como ya sabemos del Acto II, podemos resolver el problema en un grafo no dirigido, sin preocuparnos por los distintos sentidos.
Problema del viajante múltiple. Dado un grafo completo, encontrar \(N\) (en nuestro caso, \(3\)) ciclos, que comiencen en el mismo vértice de origen, y visiten todas las demás ciudades una única vez entre todos. La suma de los costes de los tres ciclos debe ser mínima.
El matemático ya se está quedando sin ideas.
Matemático.- El problema ya era complicadísimo con un viajante, y ahora resulta que tengo que poner más. Esto tiene que ser imposible, a no ser…
Al matemático se le ha ocurrido una sencilla idea para convertir el problema en el tradicional que vimos en el Acto I. Supongamos que comenzamos, por ejemplo, en este grafo:
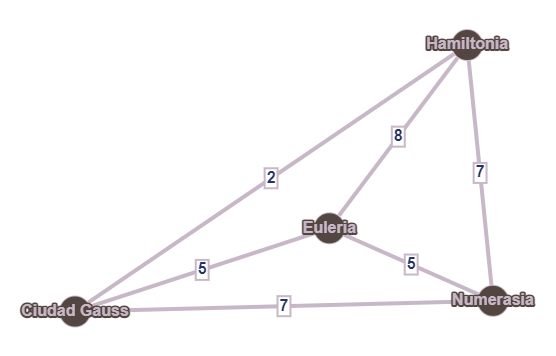
También supondremos que la ciudad donde habitan los tres viajantes es Euleria. Hemos dicho anteriormente que no podemos trocear un trayecto óptimo en tres, porque todos ellos deberían empezar y acabar en Euleria, y esta ciudad solo aparece una vez en cualquier solución. La idea del matemático es sencilla: habrá tres “copias” de Euleria:
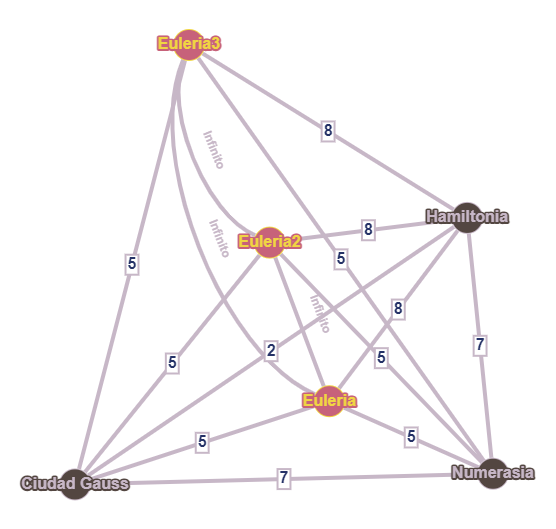
¡Qué bonito! Fijémonos además que la distancia entre las copias es infinita: así, no podrá haber dos seguidas en un camino óptimo. Ahora, resolvemos el ciclo hamiltoniano óptimo para todo el grafo:
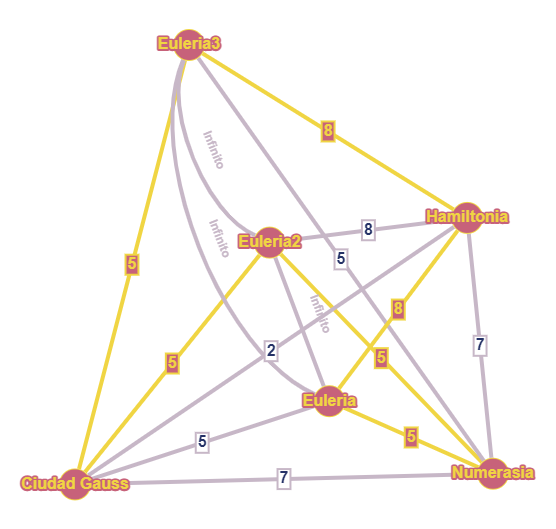
Ha salido Euleria - Numerasia - Euleria2 - Ciudad Gauss - Euleria3 - Hamiltonia, con coste total \(5+5+5+5+8+8 = 36\). Ahora, lo único que hay que hacer es que cada viajante recorra uno de los tramos que quedan separados por las distintas copias. Es decir, ¡ahora sí podemos dividir en tres el camino!. Uno de los viajantes hará Euleria - Numerasia - Euleria, el otro Euleria - Ciudad Gauss - Euleria, y el último Euleria - Hamiltonia - Euleria. La suma de los costes es la que habíamos obtenido, \(36\).
Matemático.- Creo que con este mecanismo lo he conseguido. Ya tengo la solución para el vendedor, y lo bueno es que solo he tenido que reducirlo al problema original, de nuevo. Es imposible que este problema pueda complicarse aún más. Bueno, podría buscar que la ruta más larga de las tres fuese de distancia mínima, y no la suma de todas ellas, pero creo que por ahora voy a pasar del tema.
Acto IV. Satisfaciendo necesidades.
(De noche. Llaman a la puerta.)
Matemático.- Zzz…
Vendedor ambulante.- ¡Matemático! ¡Oye! ¿Estás en casa?
Matemático.- Ya voy.
(Abre la puerta)
Matemático.- ¿Tú otra vez? ¿Qué le pasa ahora a la ruta? ¿Quieres que vaya solo entre ciudades que empiecen y acaben por la misma letra? ¿Que haya una estación de tu gasolinera favorita cada exactamente cinco ciudades? ¿O acaso minimizar el coste de los peajes?
Vendedor ambulante.- Lo último no me importaría, pero no es eso. Verás, a uno de mis empleados le encanta esta ciudad…
(Señala una ciudad en el mapa. Solo la ve el matemático, para evitar controversias).
Matemático.- Bueno, pues dale a él la ruta que pasa por esa ciudad, ¿no crees?
Vendedor ambulante.- Es que, verás… A mí también me gustaría pasar por esta otra ciudad…
(Señala otra ciudad)
Vendedor ambulante.- De hecho, no es solo eso, sino que ahí necesitan las hortalizas más caras, que son las que llevo yo.
Matemático.- Pues elige tú la ruta que pasa por esa ciudad.
Vendedor ambulante.- Es la misma que la que atraviesa la ciudad favorita de mi empleado.
Matemático.- Ya es mala suerte.
Vendedor ambulante.- No te preocupes. Al lado de cada ciudad he puesto el nombre del empleado que prefiere pasar por ella, si se da el caso. No son muchas, pero…
Matemático.- Me vuelvo a la cama.
Vendedor ambulante.- ¡Espera! Por favor, encuéntrame rutas optimizadas que resuelvan nuestras preferencias. Te pagaré bien.
Como es habitual, el matemático tiene que modificar el problema para que se ajuste a las necesidades del vendedor. Es fácil hacerlo mediante colores. El matemático asigna a cada empleado un color. Después, cada vértice es coloreado con el color del empleado que lo prefiere, si es que hay alguno. Por los vértices coloreados deberá pasar el empleado correspondiente. El problema se convierte en:
Problema del viajante coloreado. Dado un grafo completo, donde cada vértice puede (o no) estar coloreado con uno de \(N\) colores distintos (en nuestro caso, \(3\)), encontrar \(N\) ciclos (en nuestro caso, \(3\)), que comiencen en el mismo vértice de origen, no coloreado, y visiten todas las demás ciudades una única vez entre todos. La suma de los costes de los tres ciclos debe ser mínima. Cada ciclo tendrá asociado uno de los \(N\) colores. Por los vértices coloreados solo podrá pasar el ciclo del mismo color. Por los vértices sin colorear, podrá pasar cualquier ciclo.
Matemático.- Es muy difícil resolver este problema. Se me ocurre una manera de hacerlo cuando todos los vértices están coloreados con alguno de los colores. Os la contaré a continuación.
Para explicarlo, el matemático parte del siguiente grafo de ejemplo:
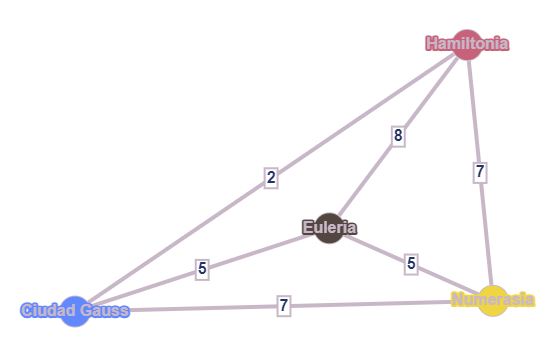
Como ha mencionado, todos los vértices están coloreados de alguno de los tres colores, a excepción del punto de partida, Euleria, que no puede estar coloreado porque todos deben empezar allí. Ahora, hace el truco habitual de triplicar el punto de partida, y como cada una de las copias representa un empleado, las colorea cada una con un color (el correspondiente al empleado):
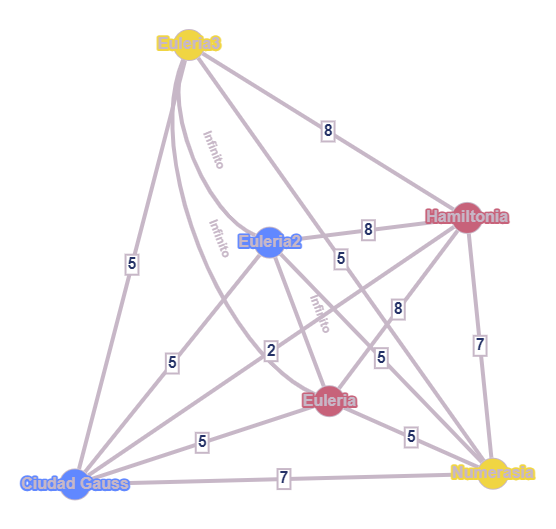
Así, el empleado que empieza desde Euleria es el rojo, el de Euleria2 es el azul y el de Euleria3 es el amarillo.
Matemático.- El truco es el siguiente. Voy a eliminar todas las aristas que conectan nodos de distinto color. Así, cada empleado solo podrá quedarse en su color, evitando que cambie al color equivocado.
Como ha explicado el matemático:
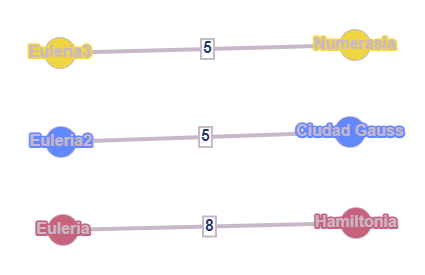
Ahora, el problema es fácil, puesto que se obtienen tres grafos distintos, y se puede resolver el problema original del Acto I en cada uno de ellos. En estos grafos concretos es muy fácil, al solo haber dos vértices en cada uno. Se obtienen así las tres rutas deseadas Euleria - Hamiltonia - Euleria, Euleria - Ciudad Gauss - Euleria y Euleria - Numerasia - Euleria. El coste es, si tenemos en cuenta volver a Euleria, \(5+5+5+5+8+8 = 36\).
Acto V. Epílogo.
Matemático.- Gracias por pagarme por mis esfuerzos. Creía que no tendrías tiempo, con todo lo que viajas.
Vendedor ambulante.- Es lo menos que puedo hacer. Aunque, tengo una última pregunta…
Matemático.- (Palidece).
Vendedor ambulante.- ¿Cómo haces para resolver todas las locuras que se me ocurren?
FIN.
Referencias.
- Algoritmo de Christofides
- R. Kumar, H. Li. Transformation to Symmetric TSP and Performance Bound
- T. Bektas. The multiple travelling salesman problem: an overview of formulations and solution procedures.
- Y. Lu, J. Hao, Q. Wu. Solving the Clustered Travelling Salesman Problem via TSP methods.
- Grafo inicial de la Península Ibérica.
- Editor interactivo de grafos